Ο ‘Ιππασος ο Μεταποντινός ήταν Πυθαγόρειος φιλόσοφος, μαθηματικός και φυσικός. Η μεγαλύτερη ανακάλυψή του ήταν η τετραγωνική ρίζα. Αυτή όμως η ανακάλυψη ήταν αρκετά «επικίνδυνη» εκείνη την περίοδο.
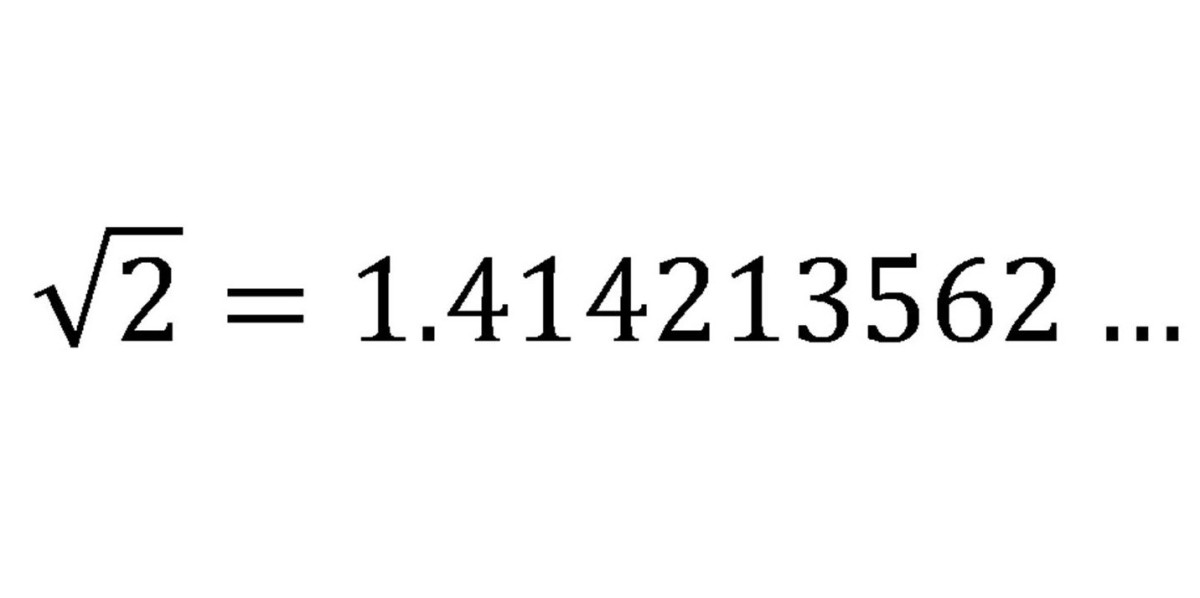
Η ισχυρότερη πεποίθηση των Πυθαγόρειων ήταν πως όλο το Σύμπαν, εκφράζεται με ρητούς αριθμούς - ρητός αριθμός είναι ο αριθμός που μπορεί να εκφραστεί ως πηλίκο δύο ακέραιων αριθμών, δηλαδή ως κλάσμα. Αυτό δεν αποτελούσε απλά μια θεωρία, ήταν ο θεμέλιος λίθος πάνω στον οποίο οι Πυθαγόρειοι είχαν χτίσει την δική τους ερμηνεία για το πώς λειτουργούν τα πράγματα. Πίστευαν πως οι αριθμοί δεν είναι απλά σύμβολα, αλλά κάτι θεϊκό που μας βοηθάει να μετράμε και να υπολογίζουμε. Ακόμα και η λέξη «ρητός» αριθμός προέρχεται από τη λέξη «ρήτρα» και υποδηλώνει ότι οι αριθμοί αυτοί μπορούν να εκφραστούν ρητά, δηλαδή με σαφήνεια και ακρίβεια.
Το «πρόβλημα» με την τετραγωνική ρίζα του Ίππαρχου ήταν πως στην ουσία είχε ανακαλύψει τον πρώτο άρρητο αριθμό! Δηλαδή έναν αριθμό με άπειρα δεκαδικά ψηφία. Η ειρωνεία στην υπόθεση ήταν πως ο Ίππασος έφτασε σε αυτό το συμπέρασμα χρησιμοποιώντας ως βάση το Πυθαγόρειο θεώρημα και τους ρητούς αριθμούς καταλήγοντας σε άτοπο. Η απόδειξη του Ίππασου αναφέρεται από τον Αριστοτέλη ως χαρακτηριστικό παράδειγμα χρήσης της «εις άτοπον απαγωγής».
Για όσους θέλουν να φρεσκάρουν τα μαθηματικά τους…
Αριθμοί: Οι αριθμοί είναι μαθηματικά αντικείμενα που χρησιμοποιούνται για τη μέτρηση, την αρίθμηση και τον υπολογισμό ποσοτήτων. Οι αριθμοί χωρίζονται σε σύνολα (το καθένα με δικές του ιδιότητες) όπως οι φυσικοί αριθμοί, οι ακέραιοι αριθμοί, οι ρητοί αριθμοί, οι πραγματικοί αριθμοί, οι μιγαδικοί αριθμοί και πολλοί άλλοι.
Φυσικοί αριθμοί: Σύνολο αριθμών που περιλαμβάνει τους μη αρνητικούς ακέραιους αριθμούς, δηλαδή τους αριθμούς 0, 1, 2, 4, 5, 6, και ούτω καθεξής.
Ακέραιοι αριθμοί: Σύνολο αριθμών που περιλαμβάνει το μηδέν και όλους τους θετικούς και τους αρνητικούς αριθμούς, χωρίς υποδιαίρεση ή δεκαδικό μέρος. Δηλαδή του αριθμούς …, -4, -3, -2, -1, 0, 1, 2, 3, 4, …
Ρητοί αριθμοί: Υποσύνολο των πραγματικών αριθμών που περιλαμβάνει τους ακέραιους και όλους τους αριθμούς που μπορούν να εκφραστούν ως πηλίκο δύο ακέραιων αριθμών, δηλαδή τα κλάσματα. Για παράδειγμα το 5 (ακέραιος) είναι και ρητός γιατί μπορεί να εκφραστεί ως πηλίκο 5/1. Η τιμή -2,75 είναι ρητός γιατί μπορεί να εκφραστεί ως πηλίκο -11/4
Άρρητοι αριθμοί: Οι αριθμοί που δεν μπορούν να εκφραστούν ως πηλίκο δύο ακέραιων αριθμών. Οι άρρητοι αριθμοί είναι απειροστοί και δεν μπορούν να αναπαρασταθούν με ακριβή δεκαδική αναπαράσταση, δηλαδή έχουν άπειρα δεκαδικά ψηφία.
Πρώτοι αριθμοί: Είναι φυσικοί αριθμοί μεγαλύτεροι της μονάδας, που διαιρούνται μόνο με τον εαυτό τους και το 1, δηλαδή δεν έχουν άλλους διαιρέτες εκτός από τον εαυτό τους και το 1. Παραδείγματα πρώτων αριθμών είναι το 2, το 3, το 5, το κ.λ.π.
Άρτιοι αριθμοί: Υποσύνολο των ακέραιων αριθμών, που όταν διαιρούνται με το 2 δίνουν αποτέλεσμα ακέραιο. Λόγω αυτής της ιδιότητας κάθε ακέραιος όταν πολλαπλασιαστεί με το 2, γίνεται άρτιος. Για παράδειγμα 2*5 = 10, 2 * 7 = 14, 2*9 = 18, 2*11 = 22 κ.ο.κ.
Αρχική υπόθεση
Έστω ότι ο είναι ρητός, δηλαδή μπορεί να εκφραστεί ως πηλίκο δύο ακέραιων α, β πρώτων μεταξύ τους με α, β ≠ 0 (διάφοροι του μηδενός).
Από την υπόθεση προκύπτει,
Υψώνοντας και τις δύο πλευρές στο τετράγωνο έχουμε,
Παρατηρούμε ότι ο αριθμός είναι άρτιος αφού ισούται με το γινόμενο του επί 2. Αυτό με την σειρά του σημαίνει ότι αφού το 2 διαιρεί το αριστερό μέλος, τότε θα πρέπει να διαιρεί και το δεξί μέλος. Τελικά συμπεραίνουμε ότι και το α θα πρέπει να είναι άρτιος. Επομένως μπορούμε να γράψουμε τον αριθμό α ως πολλαπλάσιο του 2, δηλαδή
Με αντικατάσταση στην προηγούμενη εξίσωση έχουμε,
Διαιρώντας και τα δύο μέλη με το 2 προκύπτει,
Ακολουθώντας το ίδιο επιχείρημα με πριν το 2 διαιρεί το , άρα και ο αριθμός β είναι άρτιος. Αυτό όμως οδηγεί σε αντίθεση με την αρχική υπόθεση ότι οι αριθμοί α, β είναι πρώτοι μεταξύ τους και τελικά συμπεραίνουμε ότι ο είναι άρρητος.