Η ιστορία των αριθμών

Το ήξερες ότι οι αριθμοι εξελίσσονται μαζί με την ανθρωπότητα; Πιο συγκεκριμένα οι αριθμοί "πληθαίνουν” όσο αυξάνονται οι ανάγκες των ανθρώπων. Εντάξει τώρα με αυτό το “πληθαίνουν” μπορεί να σε μπέρδεψα όμως αυτό ακριβώς έχει συμβεί.

Ας το πάρουμε απ’ την αρχή…

Φυσικοί αριθμοί

Ανάλογα των γνώσεών σου στα Μαθηματικά, ίσως ήδη γνωρίζεις ότι οι αριθμοί χωρίζονται σε σύνολα (σε σακουλάκια όπως λέω και στον γιο μου). Το πρώτο σύνολο αριθμών (σακουλάκι) που εμφανίστηκε στην ανθρωπότητα είναι αυτό που αποκαλούμε σήμερα Φυσικοί Αριθμοί και συμβολίζεται με . 

Τα πολύ παλιά χρόνια οι αριθμοί ονομάζονταν  “αντικείμενα”, γιατί στην ουσία οι άνθρωποι χρησιμοποιούσαν την αρίθμηση μόνο για να μετράνε αντικείμενα. Έτσι λοιπόν ο άνθρωπος οδηγήθηκε στην δημιουργία των απόλυτων και τακτικών αριθμών.

Οι απόλυτοι αριθμοί ή αλλιώς οι πληθάριθμοι είναι αυτοί που εκφράζουν πλήθη και πολύ γρήγορα η ανθρωπότητα προχώρησε στην ιδέα της σύγκρισης για αντικείμενα, ζώα, ανθρώπους. Έτσι με την πάροδο του χρόνου δημιουργήθηκαν οι εκφράσεις “Αυτός ο σωρός έχει περισσότερες πέτρες από εκείνον τον σωρό”,  “Αυτό το κοπάδι έχει λιγότερα ζώα από εκείνο το κοπάδι” κτλ. 

Στην συνέχεια η ανάγκη (πάλι) οδήγησε τους ανθρώπους να δημιουργήσουν μια “ιεράρχηση” εντός του ενός και του άλλου συνόλου αντικειμένων. Για παράδειγμα στους Ολυμπιακούς Αγώνες όλοι οι αθλητές του άλματος εις μήκος ήταν τα “αντικείμενα” ενός συγκεκριμένου συνόλου και με κάποιον τρόπο έπρεπε να ξέρουν ποιος ήρθε πρώτος, δεύτερος, τρίτος. Έτσι λοιπόν δημιουργήθηκαν οι τακτικοί αριθμοί. Με άλλα λόγια οι τακτικοί αριθμοί είναι αριθμοί θέσεως: 1ος, 2ος, 3ος,... .

Εδώ έχει αξία να πούμε ότι οι τακτικοί αριθμοί έχουν την σημασία της διάταξης, της κατάταξης, της ιεράρχησης οπότε ανάλογα με την περίπτωση οι άνθρωποι έπρεπε να βάζουν και συγκεκριμένα κριτήρια. Όπως το παράδειγμα με τους αθλητές, το κριτήριο για το ποιος θα είναι 1ος ήταν το μέγιστο άλμα. 

Αυτά τώρα ίσως σου φαίνονται απλά και αυτονόητα, όμως πρέπει να τοποθετήσεις τον εαυτό σου σε έναν κόσμο όπου τίποτα από τα παραπάνω δεν υπάρχει για να κατανοήσεις το μεγάλο άλμα της ανθρωπότητας όταν δημιουργήθηκαν οι Φυσικοί Αριθμοί. 

Με τα χρόνια ορίστηκαν οι πράξεις και οι ιδιότητες των Φυσικών Αριθμών. Όσο και να σου κάνει εντύπωση δεν μπορείς να κάνεις όλες τις πράξεις όταν το αποτέλεσμα ανήκει στους φυσικούς αριθμούς. Να θυμάσαι ότι το σύνολο των φυσικών αριθμών περιέχει τους αριθμούς από το 0 κατά άλλους από το 1 έως το συν άπειρο. 

Έτσι για παράδειγμα η πράξη:  δεν είχε κανένα απολύτως νόημα, καθώς ο αριθμός τότε δεν υπήρχε ούτε σαν ιδέα, ενώ σήμερα λέμε ότι δεν ανήκει στους Φυσικούς Αριθμούς (με μαθηματική γραφή,).

Ακέραιοι αριθμοί

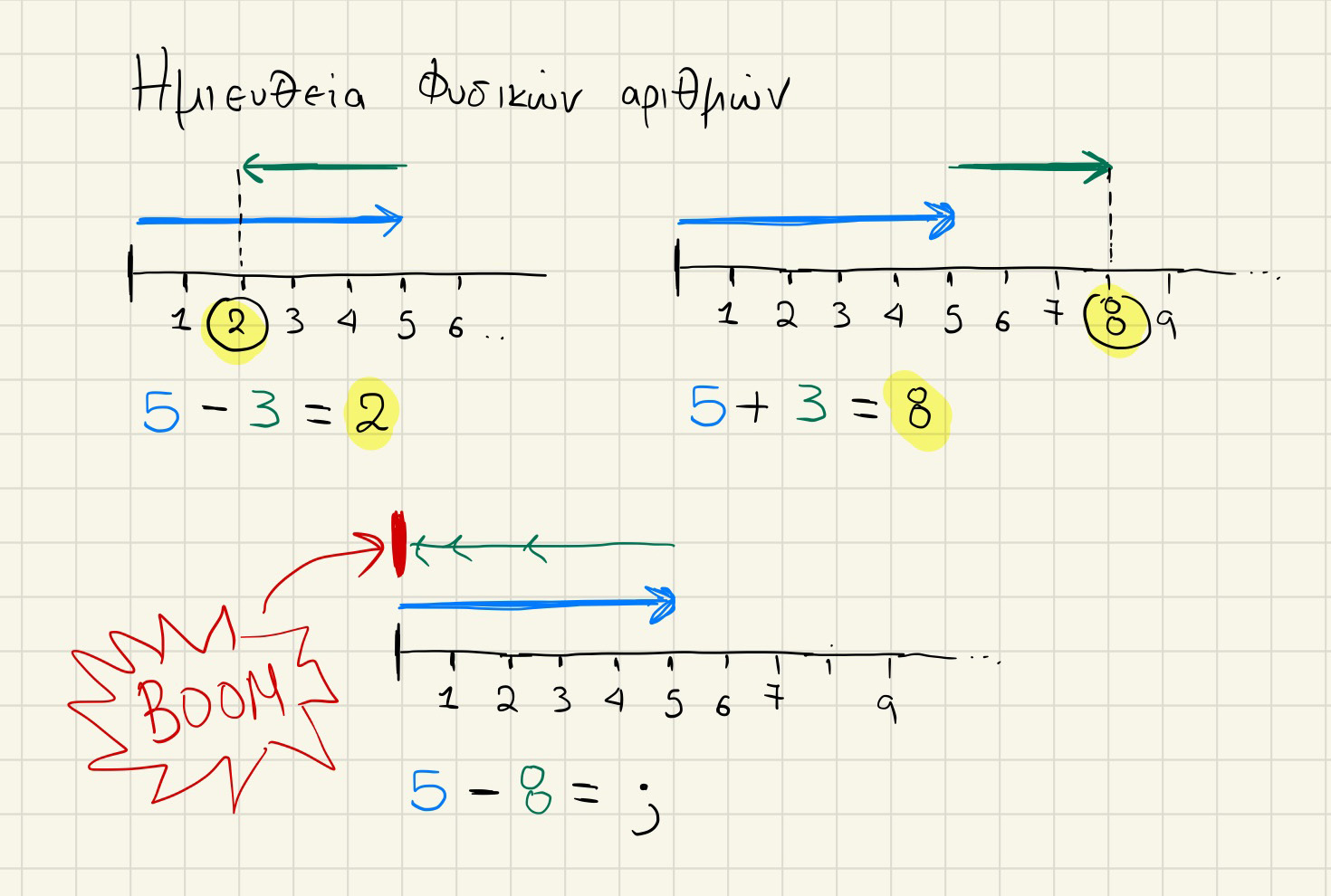
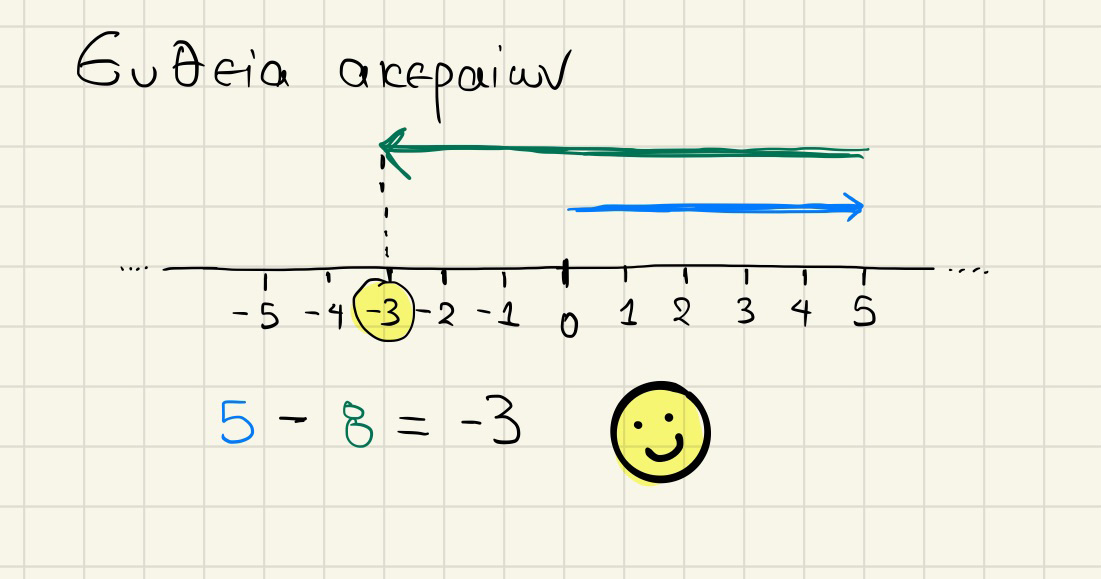
Η ανθρωπότητα εξελίσσεται κι άλλο και οι άνθρωποι διαπιστώνουν ότι πρέπει να μετρήσουν μεγέθη όπως η θερμοκρασία για παράδειγμα ή ακόμα πιο πρακτικά πράγματα όπως στα οικονομικά. Δηλαδή αν μιλάμε για 1000 ευρώ σε έναν άνθρωπο, τι εννοούμε; Χρεωμένα ή Πιστωμένα; Ή όταν λέμε 300 μέτρα από την επιφάνεια της θάλασσας, πρόκειται για άνωθεν ή κάτωθεν; 

Ωστόσο ιστορικά φαίνεται ότι οι αρχαίοι πολιτισμοί αντιμετώπισαν διαφορετικά αυτό το παράξενο φαινόμενο των αρνητικών αριθμών. Σε γενικές γραμμές μπορούμε να πούμε ότι αιωρούνταν σαν ιδέα, αλλά μέχρι εκεί. 

Για παράδειγμα οι αρχαίοι Έλληνες δεν αντιμετώπισαν πραγματικά το πρόβλημα των αρνητικών αριθμών. Τα Μαθηματικά τους βασίζονταν σε Γεωμετρικές ιδέες. Μήκη, εμβαδόν, όγκοι, τρίγωνα, γεωμετρικές κατασκευές όλα αυτά αναγκαστικά είναι θετικοί αριθμοί. Οι αποδείξεις τους αποτελούσαν λογικά επιχειρήματα βασισμένα στην ιδέα του μεγέθους. Τα μεγέθη παριστάνονται με γραμμές ή περιοχές και όχι με αριθμούς. Με αυτόν τον τρόπο μπόρεσαν να ασχοληθούν με άλλους “αμήχανους” αριθμούς όπως οι τετραγωνικές ρίζες. 

Από τι πρώτες γραπτές αναφορές (αν όχι η πρώτη) με αρνητικούς αριθμούς έρχεται το 200 π.Χ. από την Κίνα. Με κόκκινο χρώμα αναπαριστώνται οι θετικοί αριθμοί και με μαύρο οι αρνητικοί. Τέτοιου είδους συστήματα χρησιμοποιούνταν για εμπορικούς και φορολογικούς λόγους.

Τον 3ο αιώνα μ.Χ.  ο Έλληνας μαθηματικός Διόφαντος έγραψε τα “Αριθμητικά”. Στο έργο του ασχολήθηκε με την επίλυση γραμμικών εξισώσεων με πολλούς αγνώστους. Σε ένα από τα προβλήματά του έγραψε το ισοδύναμο σήμερα που το έδινε αρνητικό αποτέλεσμα, το οποίο και ονόμασε “άτοπο”. 

Ωστόσο ο Διόφαντος έχει χαρακτηριστεί “πατέρας της άλγεβρας” (η λέξη άλγεβρα δεν υπήρχε τότε, καθιερώθηκε αργότερα όπως θα διαβάσεις παρακάτω), καθώς στο έργο του υπάρχουν προβλήματα που λύνονται με εξισώσεις και συστήματα πρώτου και δευτέρου βαθμού, ενώ τυποποίησε μαθηματικά σύμβολα και χρησιμοποίησε τα κλάσματα ως πραγματικούς αριθμούς.

Τον 7ο αιώνα μ.Χ. ο Ινδός μαθηματικός Βραχμαγκούπτα μέσα από την θεωρητική μελέτη του αναφέρεται για πρώτη φορά σε μια σειρά κανόνων αντιμετώπισης των αρνητικών αριθμών. Ενώ τον 9ο αιώνα μ.Χ. στην Βαγδάτη ο Αλ-Χουαρίζμι παρουσίασε έξι τυποποιημένες μορφές για γραμμικές εξισώσεις παράγοντας λύσεις χρησιμοποιώντας αλγεβρικές μεθόδους και γεωμετρικά διαγράμματα. Με τις αλγεβρικές μεθόδους του αναγνώρισε ότι έλαβε ιδέες από το έργο του Βραχμαγκούπτα και ως εκ τούτου ήταν ευχαριστημένος με την έννοια των αρνητικών αριθμών. Ωστόσο, τα γεωμετρικά του μοντέλα (βασισμένα στο έργο των Ελλήνων μαθηματικών) τον έπεισαν ότι τα αρνητικά αποτελέσματα δεν είχαν νόημα (πώς μπορείς να έχεις αρνητικό τετράγωνο;). Ο Αλ-Χουαρίζμι έθεσε τις βάσεις για την εξέλιξη την Άλγεβρας και της Τριγωνομετρίας. Η λέξη άλγεβρα προέρχεται από το Αλ-τζαμπρ μια από τις δύο πράξεις που χρησιμοποιούσε για την επίλυση δευτεροβάθμιων εξισώσεων. Πολύ τον αναφέρουν ως τον “πατέρα της Άλγεβρας” και αρκετές επιστημονικές πηγές μοιράζουν αυτή την θέση τόσο στον Αλ-Χουαρίζμι όσο και στον Διόφαντο. 

Τόσο τον 10ο αιώνα μ.Χ. ο μαθηματικός  Abul -Wafa και τον 12ο ο Al - Samawal, χρησιμοποίησαν αρνητικούς αριθμούς. Συγκεκριμένα έως και σήμερα από κάποιους θεωρείται ότι τα γραπτά του  Abul -Wafa είναι το μόνο μέρος όπου βρέθηκαν “αυθεντικοί” αρνητικοί αριθμοί στα μεσαιωνικά αραβικά μαθηματικά. Προσπάθησε να δώσει έναν γενικό κανόνα με την περίπτωση όπου αφαίρεσε  5 από το 3 και αυτό του έδωσε ένα “χρέος” των 2.

Στην Ευρώπη τον 15ο-16ο αιώνα, συγκεκριμένα στην Ιταλία, όπου μεταφράζουν Βυζαντινά και Αραβικά κείμενα οι παλιές ιδέες αναβιώνουν. Όμως πολλοί μαθηματικοί κρατούν μυστικές τις μεθοδολογίες επίλυσης και οι ίντριγκες υπερισχύουν μέσα στις επιστημονικές κοινότητες. 

Τον 17ο-18ο αιώνα οι ευρωπαίοι Μαθηματικοί δεν είναι ακόμα άνετοι με την “΄έννοια” των αρνητικών αριθμών. Χαρακτηριστικό γεγονός το 1758 όταν Βρετανός Μαθηματικός Francis Maseres ισχυριζόταν οτι “Οι αρνητικοί αριθμοί σκοτεινιάζουν ολόκληρες θεωρίες εξισώσεων και καταστρέφουν πράγματα που από την φύση τους είναι υπερβολικά προφανή και απλά.”

Τελικά δεν ήταν πριν τον 19ο αιώνα όταν Μαθηματικοί όπως ο De Morgan άρχισαν να διευρύνουν τους “νόμους της αριθμητικής” ή όπως ο William Hamilton που εργαζόταν σε έναν σαφέστερο ορισμό των αρνητικών αριθμών τόσο στην αριθμητική όσο και στην Άλγεβρα. 

Τώρα μην φανταστείς ότι όλα άλλαξαν σε μια μέρα. Με αυτά και με εκείνα δημιουργήθηκε ένα νέο σύνολο αριθμών, οι Ακέραιοι. Συμβολίζονται με και περιέχουν όλους τους Φυσικούς καθώς και όλους του αρνητικούς τους, δηλαδή

Έτσι λοιπόν αποκτήσαμε τα πρόσημα και πλέον στους ακέραιους αριθμούς η αφαίρεση πάντα εκτελείται. 

Ρητοί και Άρρητοι αριθμοί 

Παρόλο που οι αρνητικοί αριθμοί άργησαν να μπουν στα Μαθηματικά οι Ρητοί αριθμοί είχαν κάνει την εμφάνισή τους από πολύ νωρίς.  Ρητοί αριθμοί είναι οι αριθμοί που μπορούν να γραφούν με μορφή κλάσματος με ακέραιο αριθμητή και ακέραιο παρανομαστή διάφορο του μηδενός ή μπορείς να πεις με παρανομαστή που ανήκει στους φυσικούς αριθμούς. Συμβολίζονται με .

Σε μαθηματική μορφή θα γράφαμε αντίστοιχα,

ή

Με απλά λόγια ρητοί αριθμοί είναι τα κλάσματα. Οι άνθρωποι γρήγορα κατάλαβαν ότι δεν είχαν όλα τα προβλήματα λύση στους φυσικούς αριθμούς, ειδικά στην καθημερινότητά τους όπως στις αγοραπωλησίες, στις ανταλλαγές προϊόντων ή ακόμα και στην μέτρηση αποστάσεων. Ακόμα και σήμερα λέμε “βάλε μου ένα τέταρτο τυρί” και εννοούμε 250 γρ. 

Ποιός εφηύρε τους Ρητούς αριθμούς; 

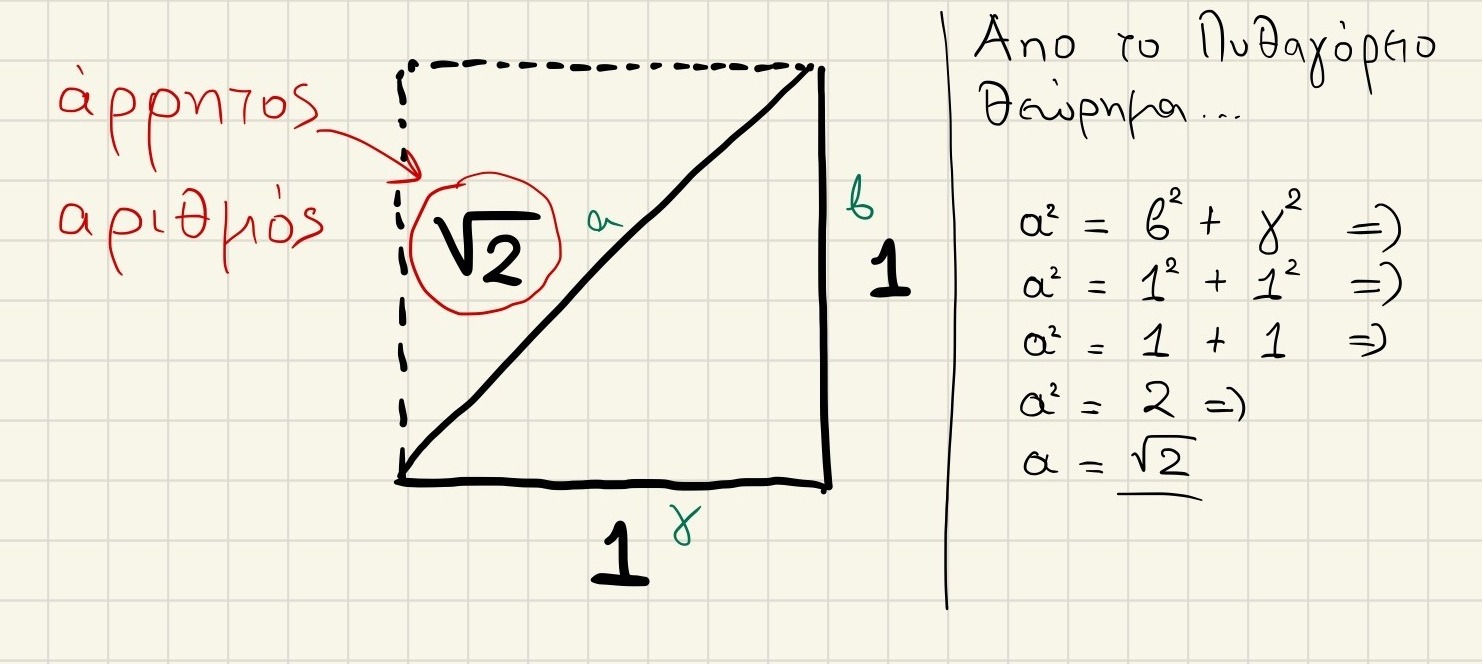
Λοιπόν, η αλήθεια είναι ότι κανείς δεν ξέρει. Αρκετά ξένα websites αποδίδουν την εφεύρεση στον Πυθαγόρα, όμως αυτό δεν αποδεικνύεται. Εκείνα τα χρόνια οι περισσότεροι επιστήμονες πίστευαν ότι οποιοσδηποτε αριθμος μπορεί να γραφτεί ως ρητός, μέσα σε αυτούς ήταν και οι Πυθαγόρειοι. Ό Ίππασος, επίσης πυθαγόρειος, με την χρήση του Πυθαγορείου θεωρήματος βρήκε και αποκάλυψε πως η διαγώνιος ενός τετραγώνου με πλευρά δεν είναι ρητός, με άλλο λόγια ανακάλυψε την , δηλαδή τους  Άρρητους αριθμούς. 

Η σύγκρουση του Ίππασου με τους Πυθαγόρειους ήταν τόσο μεγάλη που η παράδοση λέει πως τον δολοφόνησαν. Η βασική θεωρία των Πυθαγορείων ήταν πως όλο το Σύμπαν, άρα και όλοι η αριθμοί μπορούν να εκφραστούν με κλασματική μορφή. Και ενώ αναγνώρισαν την μεγάλη ανακάλυψη του Ίππασου προτίμησαν να τον δολοφονήσουν για να μην καταρρεύσει η θεωρία τους.  Έτσι οι άρρητοι αριθμοί “εξαφανίστηκαν” και έκαναν πάλι την είσοδό τους στα Μαθηματικά τον 19ο αιώνα. 

Οι Άρρητοι αριθμοί συμβολίζονται με τον έμμεσο συμβολισμό ή . Βασικό χαρακτηριστικό τους είναι ότι έχουν άπειρο αριθμό, μη επαναλαμβανόμενων περιοδικά, δεκαδικών ψηφίων. Άλλοι γνωστοί άρρητοι αριθμοί είναι το και το . Το πιο εντυπωσιακό είναι ότι οι άρρητοι αριθμοί είναι πολύ περισσότεροι από τους ρητούς. 

Πραγματικοί Αριθμοί

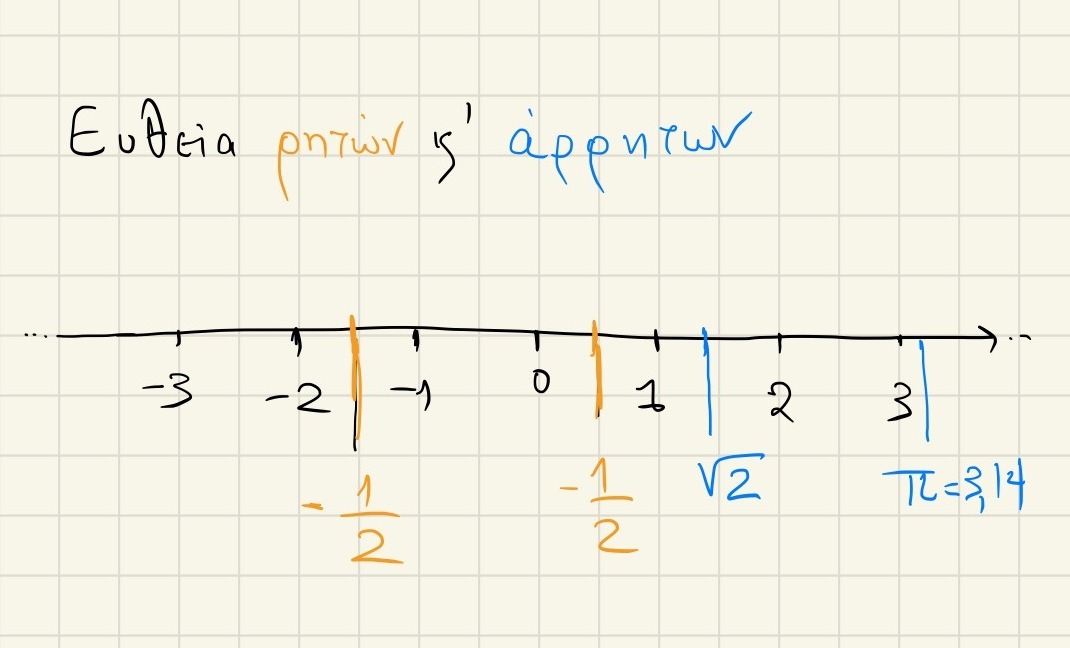
Οι Πραγματικοί αριθμοί είναι όλοι οι αριθμοί που είδαμε παραπάνω σε ένα σύνολο, το οποίο συμβολίζεται με . Δηλαδή, οι Πραγματικοί αριθμοί αποτελούνται από τους Φυσικούς, τους Ακέραιους, τους Ρητούς και τους Άρρητους. 

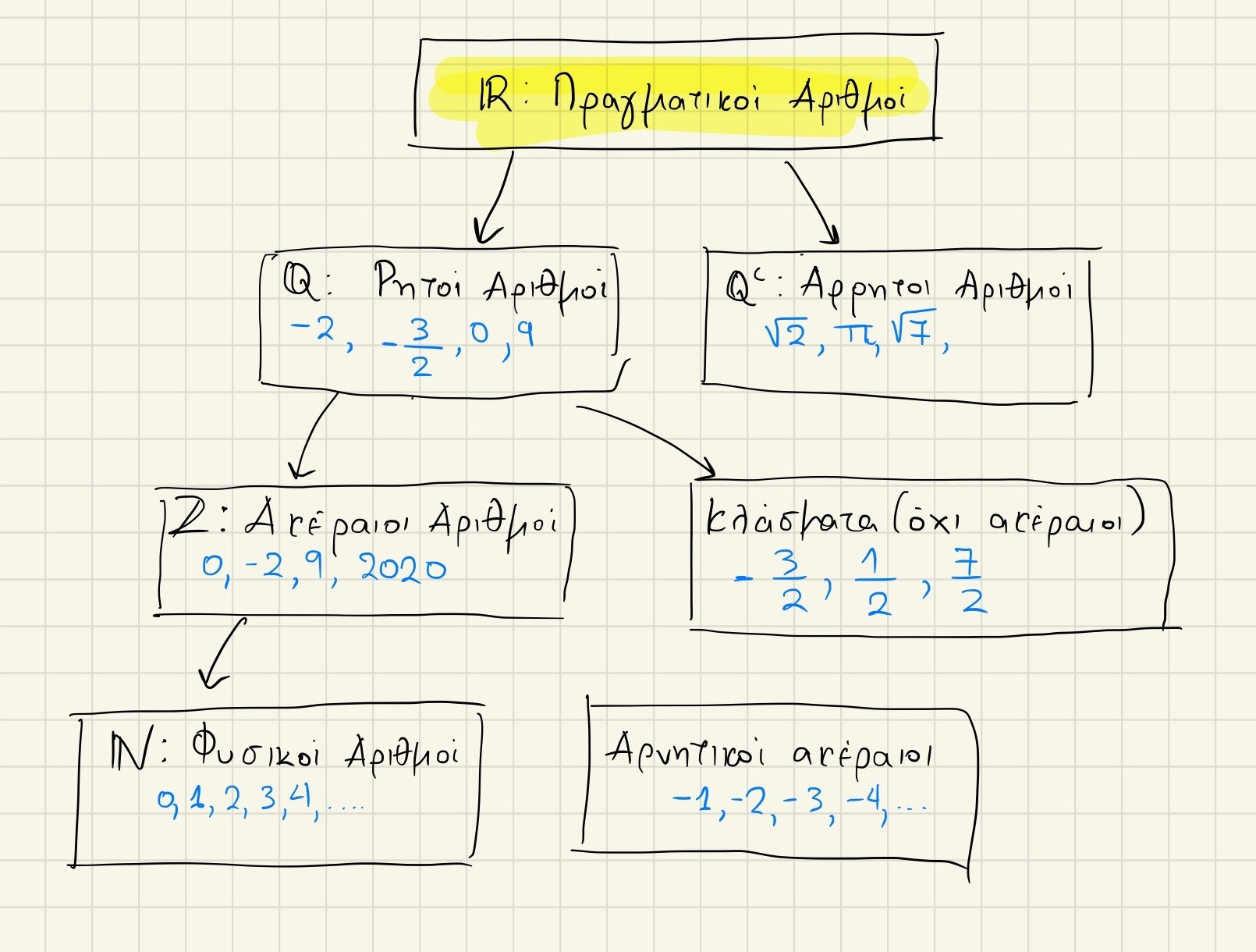
Πλέον πάνω σε μία ευθεία (συγκεκριμένα στην ευθεία των Πραγματικών Αριθμών) μπορούμε να αναπαραστήσουμε οποιονδήποτε αριθμό. Με άλλα λόγια όποιο σημείο κι αν επιλέξεις πάνω στην ευθεία, αντιπροσωπεύεται από έναν μοναδικό Πραγματικό Αριθμό. 

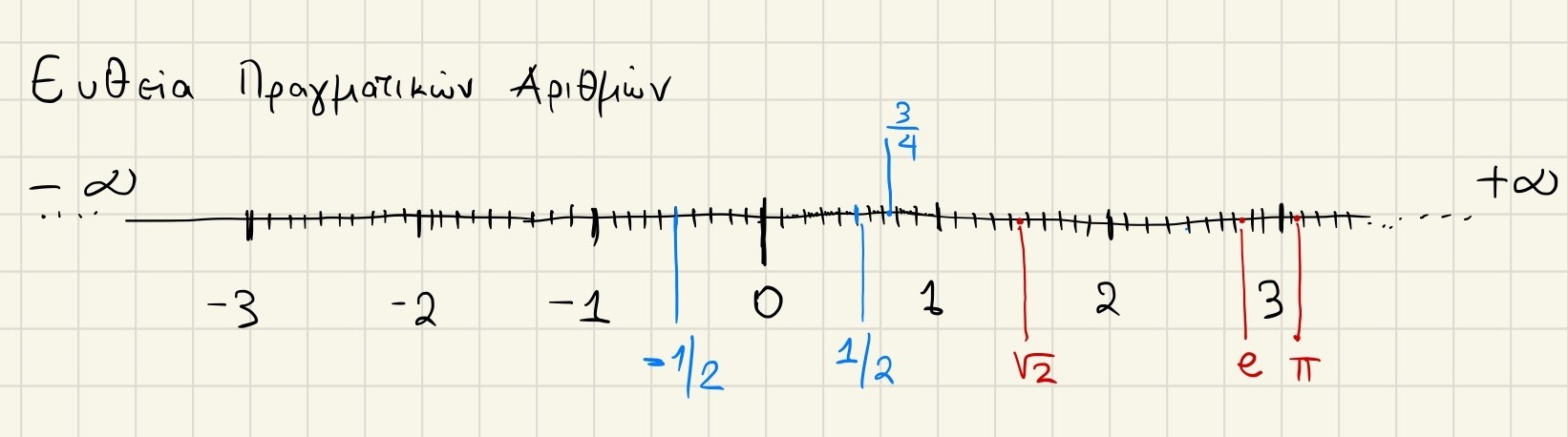
Ωστόσο η ανάγκη όλοι αυτοί οι αριθμοί να μπουν σε ένα “επίσημο’ σύνολο με το όνομα Πραγματικοί, δημιουργήθηκε τον 17ο όταν χρειάστηκε να τους “ξεχωρίσουν” απο τους φανταστικούς αριθμούς, τους οποίους θα δούμε παρακάτω.

Μιγαδικοί αριθμοί

Κάποιος ίσως πιστεύει ότι με τους Πραγματικούς αριθμούς, ολοκληρώθηκαν οι αριθμοί. Όχι φυσικά! Υπάρχουν κάποιοι αριθμοί οι μιγαδικοί που αποτελούνται από αριθμούς και έναν φανταστικό αριθμό (και όχι με την έννοια... ουάου πόσο φανταστικά υπέροχος είναι αυτός ο αριθμός) οι οποίοι, αν και δυσνόητοι ακόμα και σήμερα για τους περισσότερους που δεν ασχολούνται με τα Μαθηματικά, έχουν κάνει το “ντεμπούτο” τους αρκετά νωρίς στην Ιστορία των Μαθηματικών. 

Κάθε Μιγαδικός αριθμός μπορεί να γραφτεί με την μορφή, 

και συμβολίζονται με

Ας κοιτάξουμε λίγο καλύτερα από τι αποτελείται,

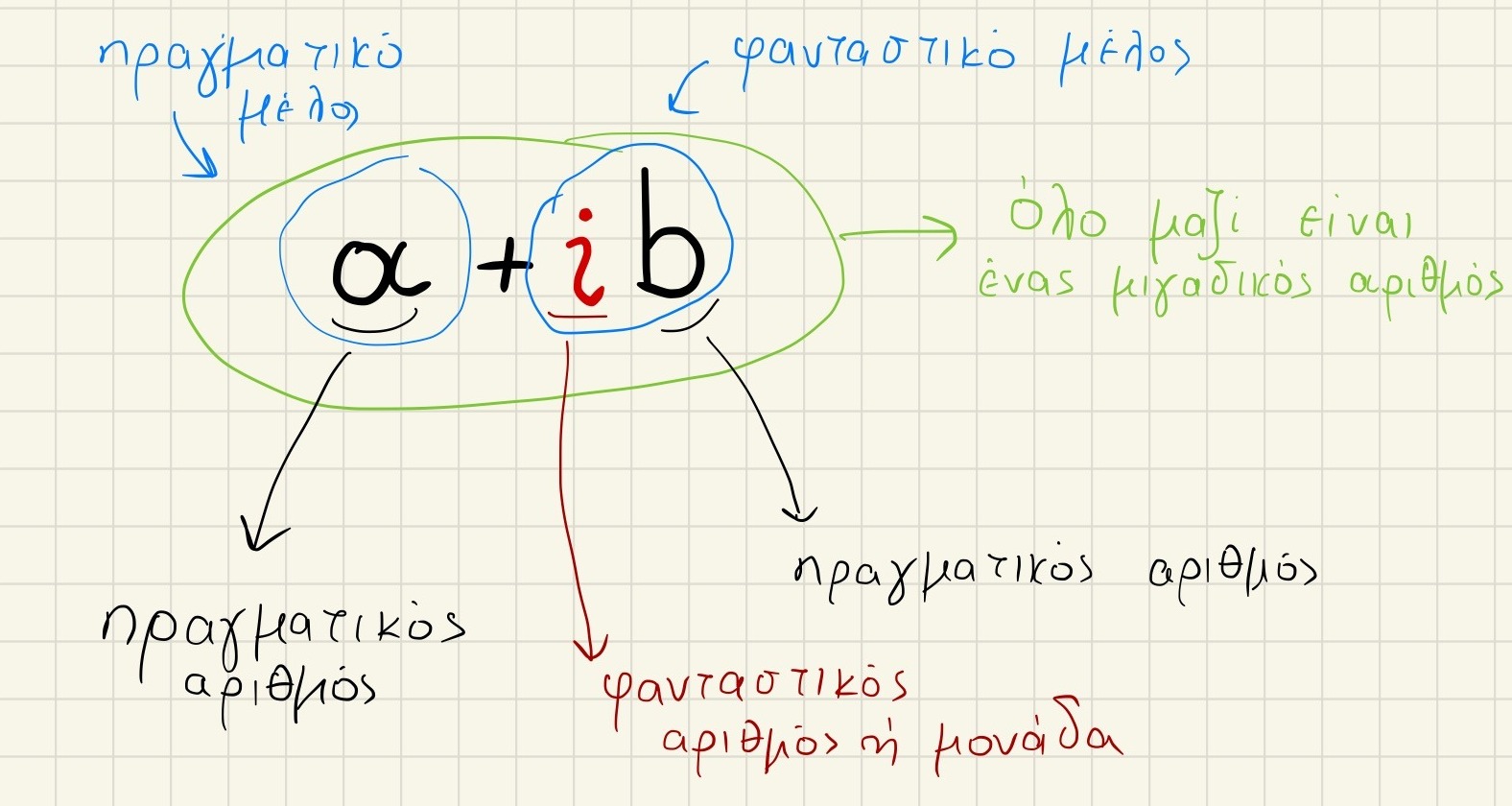
Το ονομάζεται φανταστικός αριθμός ή φανταστική μονάδα και ισούται με -1 (i = -1) με την εξής ιδιότητα

Από τα μαθηματικά θυμάσαι ότι , οπότε τώρα καταλαβαίνεις γιατί το το αποκαλούμε φανταστικό αριθμό. Η ιδιότητα αυτή ισχύει μόνο στο σύνολο των Μιγαδικών Αριθμών. 

Τώρα, ίσως όλα αυτά σου φαίνονται περίεργα και περιττά. Ίσως σκέφτεσαι “Και που χρειάζονται; Έχει νόημα αυτός ο αριθμός; ”. Λοιπόν κι όμως οι φανταστικοί (ή μιγαδικοί αριθμοί) έχουν πολλές εφαρμογές στην πραγματική ζωή όπως η ηλεκτρική ενέργεια, η επεξεργασία σημάτων, οι τετραγωνικές εξισώσεις, ενώ είναι πολύ χρήσιμοι για προηγμένους υπολογισμούς. 

Αν τώρα αναρωτιέσαι αν όντως υπάρχουν οι Μιγαδικοί Αριθμοί, τότε ίσως πρώτα θα πρέπει να αναρωτηθείς αν υπάρχουν και οι Αρνητικοί Αριθμοί. Αυτό που θέλω να πω είναι ότι δεν είναι όλοι οι αριθμοί απτοί και για να είμαι ειλικρινής δεν ξέρω τι εννοούμε με την λέξη “υπάρχουν”. Αν ψάξεις γύρω σου, ανάμεσα σε αντικείμενα μάλλον δεν θα βρεις τον -376 ή τον , ωστόσο δεν σημαίνει πως δεν “υπάρχουν”. 

Οπότε απλά να θυμάσαι ότι η φανταστική μονάδα i, διευρύνει το σύνολο των αριθμών και έτσι δημιουργήθηκαν οι Μιγαδικοί Αριθμοί. 

Ιστορικά τώρα, ο Έλληνας Μαθηματικός και Μηχανικός Ήρων έχει σημειωθεί ως ο πρώτος που έχει συλλάβει τους Μιγαδικούς αριθμούς. To 1545 -1550 εμφανίστηκαν πάλι σε γραπτά του Gerolamo Cardano και το 1572 ο Rafael Bombelli καθόρισε κανόνες για τον πολλαπλασιασμό μιγαδικών αριθμών. 

Έχει αξία να πούμε ότι ο Cardano, έκανε συστηματική χρήση των αρνητικών αριθμών (ακόμα δεν είχαν καθιερωθεί) και έγραψε σύγγραμμα με τίτλο “Βιβλίο των τυχερών παιγνίων”, το οποίο περιέχει την πρώτη συστηματική μελέτη της θεωρίας των πιθανοτήτων. 

Εκείνη την εποχή οι φανταστικοί αριθμοί και οι αρνητικοί δεν ήταν κατανοητοί και από ορισμένους θεωρούνταν ως πλασματικοί ή ακόμα και άχρηστοι, όπως κάποτε ίσχυε και για το μηδέν. Η χρήση μιγαδικών αριθμών δεν έγινε ευρέως αποδεκτή έως ότου εμφανίστηκε ο Euler (1707-1783) και ο Gauss (1777-1855).

-------------------

Αυτή ήταν εν συντομία η Ιστορία των Αριθμών, ελπίζω διαβάζοντας αυτό το άρθρο να έμαθες κάτι καινούριο.

Πάντως έχω μια απορία:
Άραγε υπάρχει κάτι πέρα από τους μιγαδικούς αριθμούς;

Με συμπαντικούς χαιρετισμούς,
Αλεξάνδρα Μαξούρα