Αυτή την εποχή αρκετοί από εμάς είχαμε την ευκαιρία να δούμε περισσότερο χιόνι. Το χιόνι ως γνωστόν αποτελείται από χιονονιφάδες όμως δεν είναι όλες παγωμένες, υπάρχει και μία χιονονιφάδα που κάνει την διαφορά. Έχει την περίεργη ιδιότητα να είναι άπειρη σε περίμετρο, αλλά ταυτόχρονα να «ζει» σε πεπερασμένη περιοχή – δηλαδή να έχει πεπερασμένο εμβαδόν.
Αυτή είναι η χιονονιφάδα το Κοχ (Koch) ή αλλιώς το νησί του Κοχ ή αλλιώς fractal. Ας το πάρουμε, όμως από την αρχή…
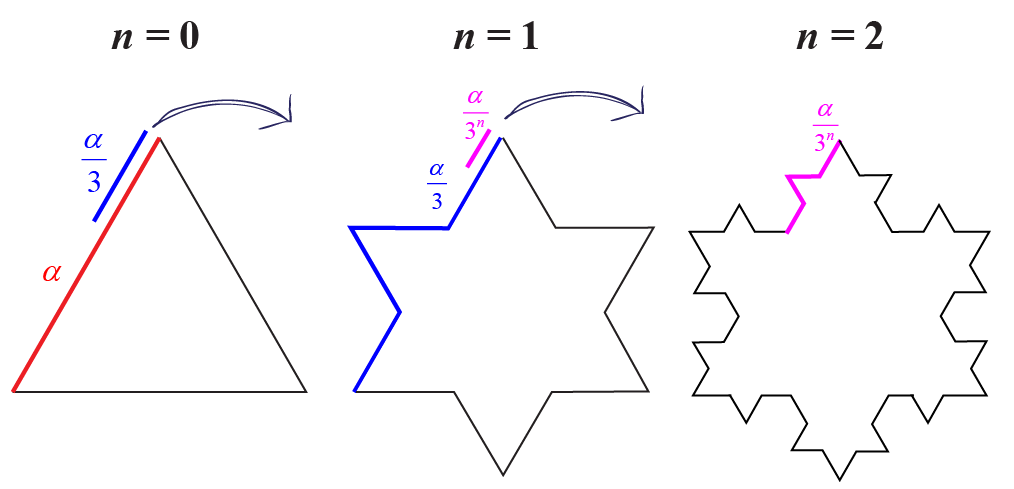
Η χιονονιφάδα το Κοχ (Koch) κατασκευάζεται χρησιμοποιώντας έναν αναδρομικό αλγόριθμο1.
Αρχίζοντας με ένα ισόπλευρο τρίγωνο, κάθε πλευρά τροποποιείται ως εξής:
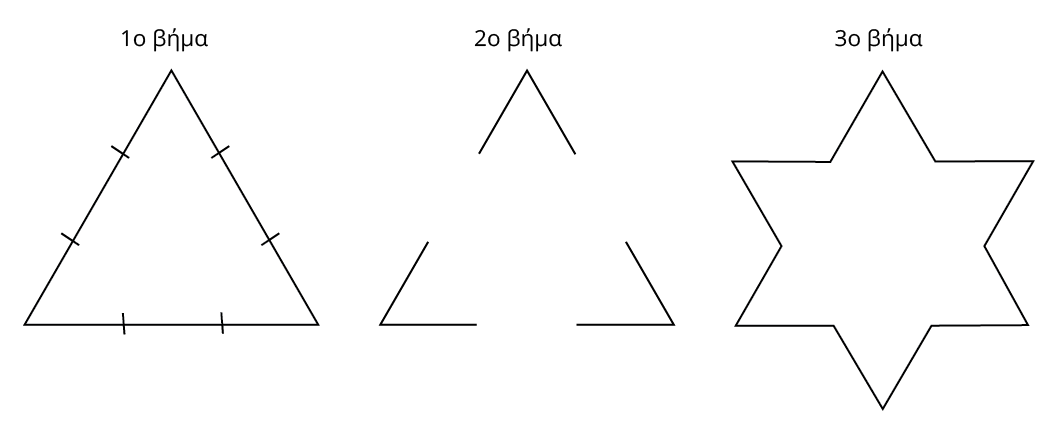
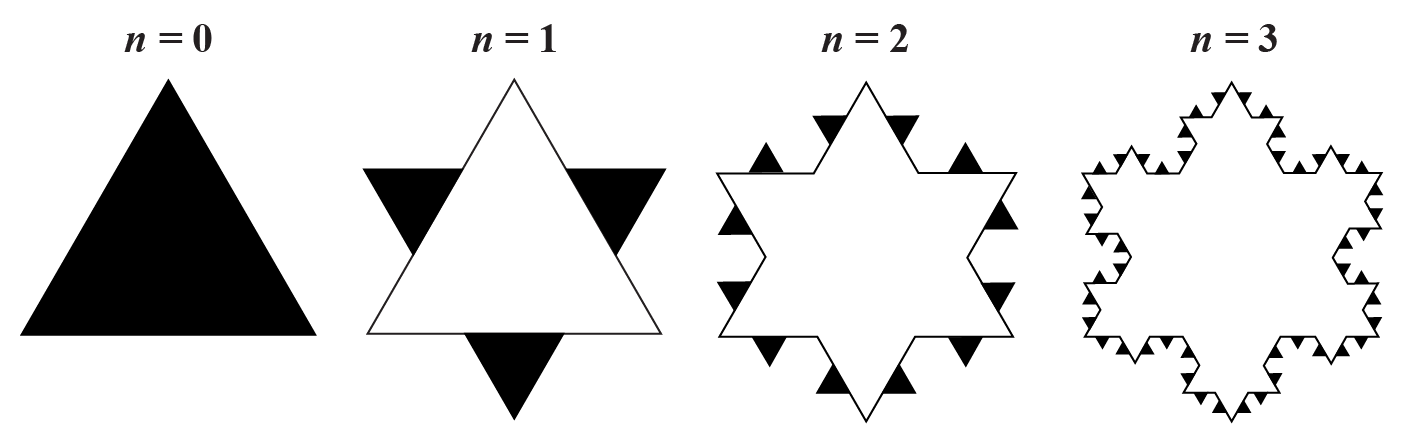
Έτσι μετά από n = 1, 2, 3, 4 επαναλήψεις η χιονονιφάδα έχει αντίστοιχα την εξής μορφή:

Όπως αναφέρουμε και πριν η χιονονιφάδα του Κοχ έχει την περίεργη ιδιότητα, να χωράει μέσα της το άπειρο.
Μετά από κάθε επανάληψη, κάθε πλευρά του ισόπλευρου τριγώνου έχει γίνει τέσσερις.
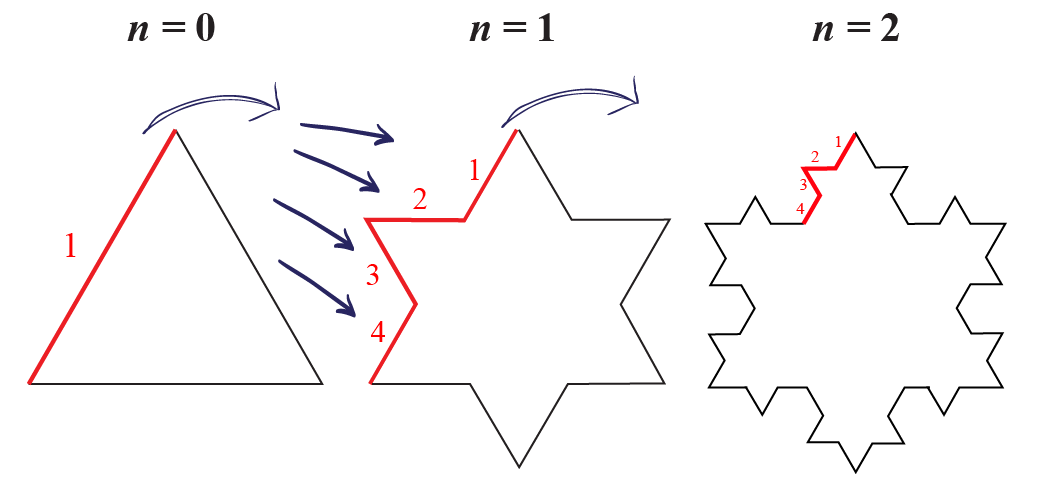
Δεδομένου ότι ξεκινάμε με 3 πλευρές, ο αριθμός των πλευρών της χιονονιφάδας στην ![]() n-οστή επανάληψη είναι:
n-οστή επανάληψη είναι:
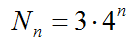
Δηλαδή, το αρχικό ισόπλευρο τρίγωνο (n = 0![]() ) έχει:
) έχει:
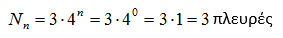
Ενώ για![]() n = 1 έχει,
n = 1 έχει,
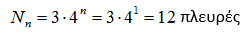
για ![]() n = 2 έχει,
n = 2 έχει,
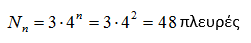
κ.ο.κ.
Μετά από κάθε επανάληψη το μήκος κάθε πλευράς είναι το 1/3 του μήκους της πλευράς της προηγούμενης επανάληψης.
Έστω ότι το μήκος της πλευράς του αρχικού ισόπλευρου τριγώνου είναι ![]() α, τότε το μήκος κάθε πλευράς στην n
α, τότε το μήκος κάθε πλευράς στην n![]() -οστή επανάληψη είναι:
-οστή επανάληψη είναι:
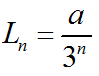
Άρα τελικά η περίμετρος της χιονονιφάδας στην n-οστή επανάληψη είναι:
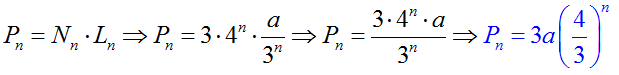
με άλλα λόγια Πλήθος Πλευρών επί Μήκος Πλευράς, δηλαδή τον μαθηματικό τύπο που χρησιμοποιούμε για τον υπολογισμό περιμέτρου των κανονικών πολυγώνων.
Έτσι λοιπόν για μήκος πλευράς α = 5cm ![]() η περίμετρος του αρχικού ισόπλευρου τριγώνου είναι 15cm
η περίμετρος του αρχικού ισόπλευρου τριγώνου είναι 15cm![]() .
.
Μετά από δύο επαναλήψεις, για n = 2![]() , η περίμετρος της χιονονιφάδας είναι:
, η περίμετρος της χιονονιφάδας είναι:
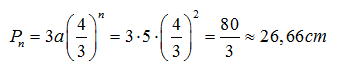
‘Ύστερα από εκατό επαναλήψεις, για n = 100, η περίμετρος της χιονονιφάδας είναι:
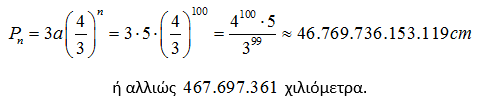
Αν σκεφτούμε ότι αυτή η περίμετρος των 467.697.361 χιλιομέτρων είναι ένα νήμα, τότε θα δούμε ότι δεν διακόπτεται πουθενά, είναι δηλαδή συνεχής. Ξεδιπλώνοντας, λοιπόν, το νήμα θα μπορούσαμε:
Αυτός ο αριθμός είναι σίγουρα πολύ μεγάλος, όμως δεν είναι το «άπειρο». Εφόσον ο αναδρομικός αλγόριθμος μπορεί να εφαρμοστεί άπειρες φορές, διαπιστώνουμε τελικά ότι η περίμετρος της χιονονιφάδας είναι άπειρη:
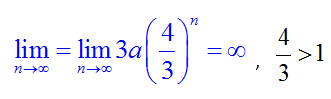
Για να υπολογίσουμε το εμβαδόν θα πρέπει να ξέρουμε πόσα τρίγωνα προστίθενται στην χιονονιφάδα μετά από κάθε επανάληψη και πόσο εμβαδόν έχει κάθε τέτοιο τρίγωνο.
O αριθμός των νέων τριγώνων που προστέθηκαν στην n-οστή επανάληψη είναι:
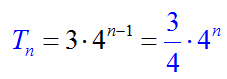
Όπως φαίνεται και στο παρακάτω σχήμα, για n = 1 προστέθηκαν 3 τρίγωνα, ενώ για n = 2![]() προστέθηκαν 12 τρίγωνα.
προστέθηκαν 12 τρίγωνα.
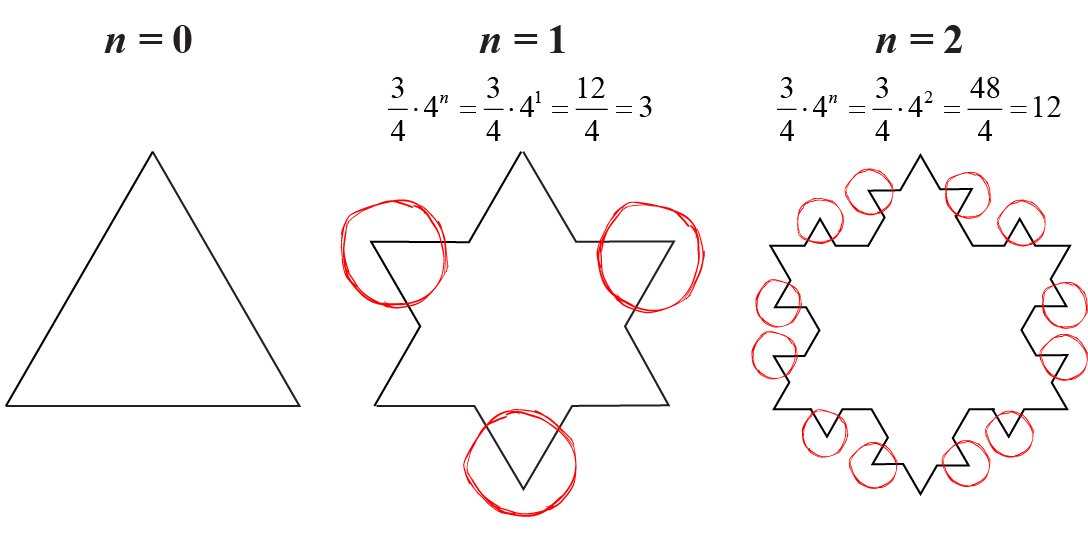
Μετά την 100η επανάληψη (n = 100), προστέθηκαν στην χιονονιφάδα:
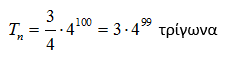
Δηλαδή, 1.205.203.533.194.242.706.656.471.569.255.871.951.891.652.245.337.094.626.476.032 τρίγωνα
Το εμβαδόν κάθε νέου τριγώνου που προστέθηκε κατά την n-οστή επανάληψη είναι το 1/9 του εμβαδού κάθε τριγώνου που προστέθηκε κατά την προηγούμενη επανάληψη (n-1)
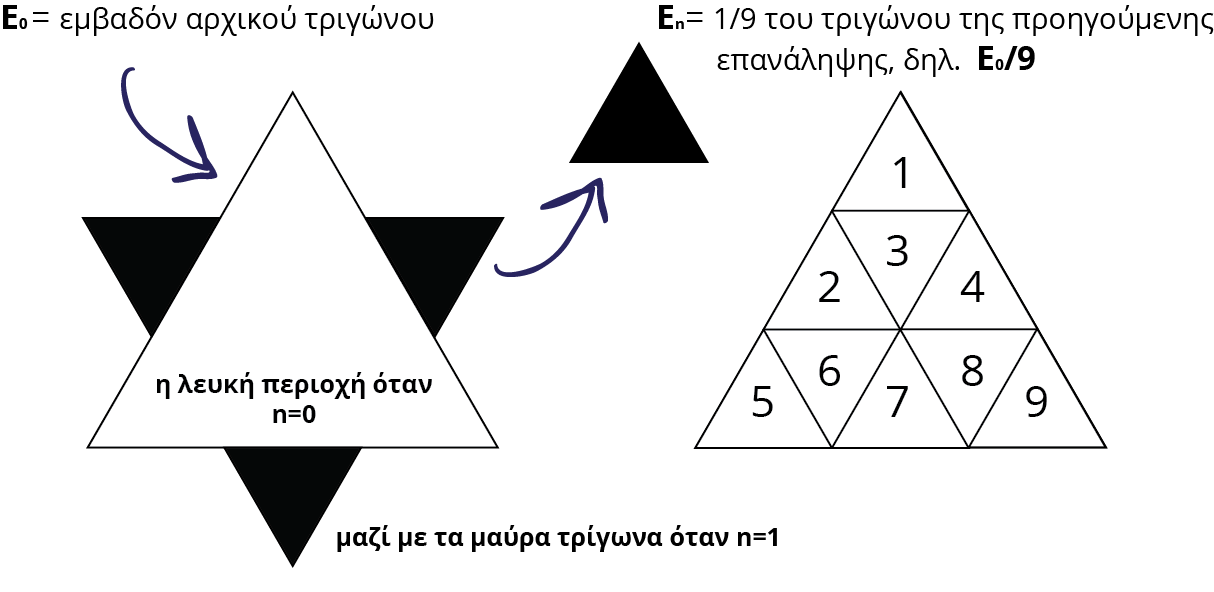
Άρα το εμβαδόν κάθε τριγώνου που προστέθηκε στην n-οστή επανάληψη είναι:
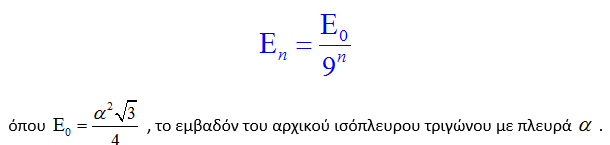
Πριν υπολογίσουμε το συνολικό εμβαδόν της χιονονιφάδας, μένει να βρούμε το συνολικό εμβαδόν που προστέθηκε στην χιονονιφάδα κατά την n-οστή επανάληψη.
Όπως φαίνεται και στην παρακάτω εικόνα, για n = 1, 2, 3 τα μαύρα τρίγωνα είναι αντίστοιχα το συνολικό εμβαδόν που προστέθηκε μετά από κάθε επανάληψη.
Έτσι π.χ. για να υπολογίσουμε το συνολικό εμβαδόν που προστέθηκε στην n-οστή επανάληψη, πολλαπλασιάζουμε τα τρίγωνα που προστέθηκαν επί το εμβαδόν κάθε τέτοιου τριγώνου.
Δηλαδή,
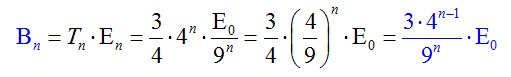
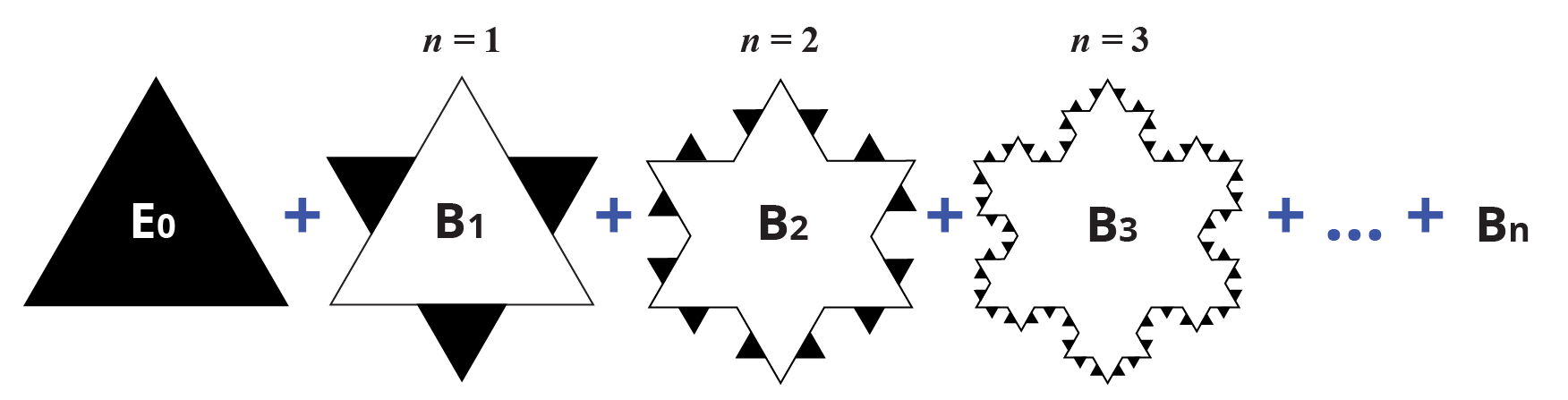
Άρα τελικά για να υπολογίσουμε το συνολικό εμβαδόν της χιονονιφάδας αρκεί να προσθέσουμε το εμβαδόν του αρχικού ισόπλευρου τριγώνου και τα συνολικά εμβαδά που προστέθηκαν στην χιονονιφάδα μετά από κάθε επανάληψη (οι περιοχές με μαύρο χρώμα):
Για παράδειγμα;
1ο Βήμα για n = 0
Αρχικά υπολογίζουμε το εμβαδόν του αρχικού ισόπλευρου τριγώνου, έστω με πλευρά α = 5cm.
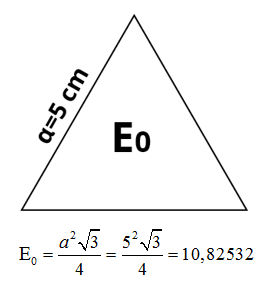
2ο Βήμα γιαm n = 1
Για να βρούμε το εμβαδόν της χιονονιφάδας μετά την 1η επανάληψη, προσθέτουμε το εμβαδόν του ισόπλευρου τριγώνου και το συνολικό εμβαδόν που προστέθηκε (οι περιοχές με μαύρο χρώμα).
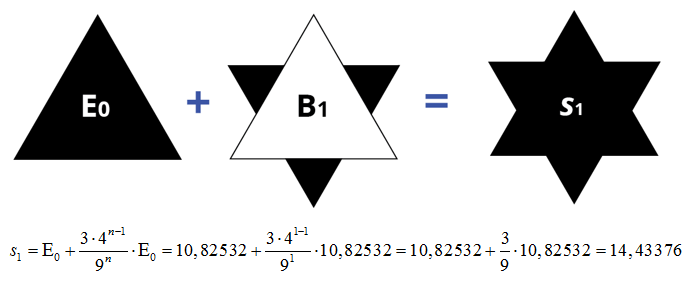
3ο Βήμα για n = 2
Με την ίδια λογική, έχουμε:
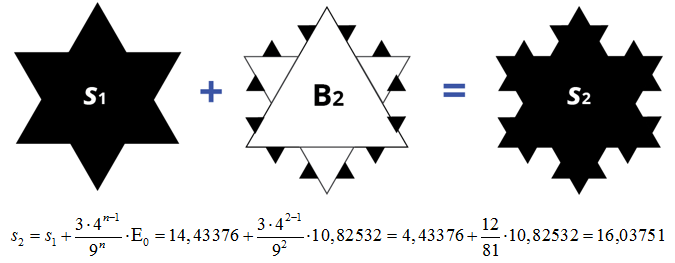
Και για την n-οστή επανάληψη έχουμε:
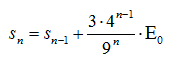
Με βάση τα προηγούμενα το συνολικό εμβαδόν της χιονονιφάδας είναι:
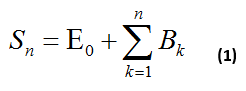
Πρόκειται δηλαδή για το άθροισμα απείρων όρων της γεωμετρικής προόδου (an = Bn) με λόγο λ.
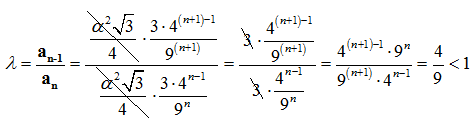
Με πρώτο όρο της σειράς:
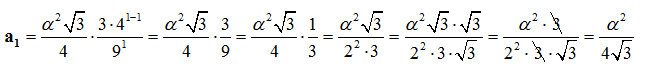
Και με n-οστό όρο:
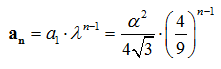
Σε αυτό το σημείο αν υπολογίζεις τους όρους a1, a2, a3 θα διαπιστώσεις ότι κάθε όρος αντιπροσωπεύει το συνολικό εμβαδόν που προστέθηκε στην χιονονιφάδα για n = 1, 2, 3 αντίστοιχα.
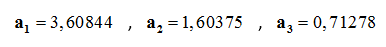
Το άθροισμα των απείρων όρων της γεωμετρικής προόδου
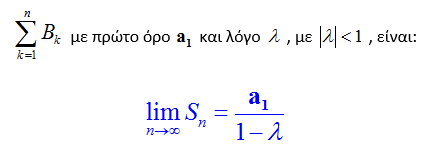
Αντικαθιστώντας στην (1), το άθροισμα της γεωμετρικής προόδου που βρήκαμε, έχουμε:
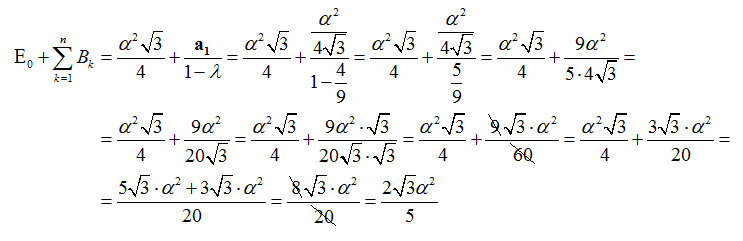
Αν λύσουμε το παραπάνω με μια διαφορετική προσέγγιση θα δούμε ότι:
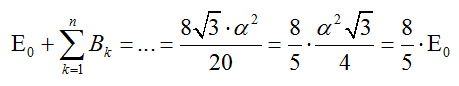
Αυτό σημαίνει ότι το εμβαδόν της τελικής χιονονιφάδας (όσο το n τείνει στο άπειρο ) είναι τα 8/5 του αρχικού εμβαδού του ισόπλευρου τριγώνου, ενώ η περίμετρος είναι άπειρη.
Καλό ε;
Let it Snow, Let it Snow, Let it Snow!
Παρακάτω δείτε ένα video (στα Ελληνικά) που εξηγεί τι είναι τα fractlas, αλλά και πως θα τα σχεδιάσετε!